【行動経済学】プロスペクト理論とは？例を使ってわかりやすく解説！

10万円を得る喜びと、10万円を失った悲しみはどちらが大きいでしょうか？

答えは10万円を失った悲しみです。

なぜ、10万円を失った悲しみの方が大きいのか？と疑問に思われるかもしれません。

この理由の根拠となるのが、ダニエル・カーネマンとエイモス・トヴェルスキーが考えたプロスペクト理論です！

今回は、このプロスペクト理論について紹介していきます！

この記事の内容をもとに、アニメーションを使った解説動画をYouTubeで挙げています！

よろしければご覧ください！

プロスペクト理論とは？

プロスペクト理論とは、自分の選択の結果から得られる利益や被る損失、それらの確率によって、人がどのような選択をするのかを記述したものです。

この理論では、人間は、利益が得られる場面では危険回避的になり、損失を被りそうなときは危険愛好的になると言われています。

プロスペクト理論には、柱となる価値関数と確率荷重関数という関数があります。

それぞれ名前に関数とついていますが、複雑な計算式が出てくるわけではないのでご安心ください笑

これから、価値関数と確率荷重関係について紹介していきます！

価値関数

まずは、次の２つの質問について、考えてみてください。

問題①

A,コインを投げて表が出たら６万円をもらうことができるが、裏が出たら何ももらえない。

B,確実に３万円がもらえる

問題②

A,コインを投げて表が出たら６万円支払い、裏が出たら何も払わない

B.確実に３万円を支払う

おそらく、問題①ではBを選び、問題②ではAを選んだという方が多いのではないでしょうか？

この問題の平均的な所得は、問題①では３万円の利得、問題②では３万円の損失となります。

我々には、平均的な利得が同じ場合であれば、確実な選択を選び、平均的な損失が同じ場合は、リスクが高い選択を選ぶ傾向があります。

これを損失回避性と言います。

ギャンブルで負けているときに、損を避けるために、さらにギャンブルをしてしまい、大金を溶かしてしまうということはよくある話です。

利得と満足度の関係と損失と満足度の関係をグラフにすると、次のようになります。

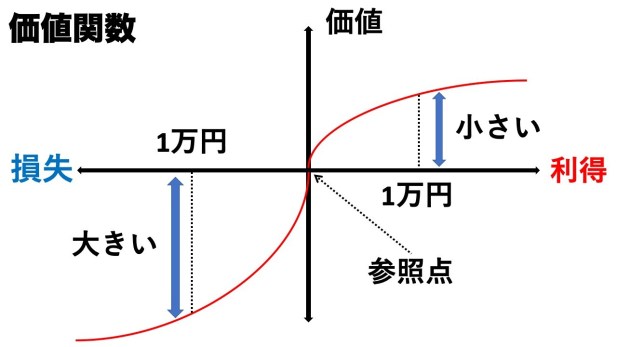
参照点とは、比較対象とする水準のことで、主に現在の所得が使われます。

横軸の右側にいけばいくほど、現在の所得と比べて利得が大きくなり、逆に左側に行くと、損失が大きくなります。

縦軸は、利得や損失によっておこる満足度の上下を表しています。

このグラフから分かることは、２つあります。

まずは、真ん中から遠さかるにつれて、線が平に近づいていることです。

そこから、お金を得る喜びや失う悲しみは、金額が大きくなるにつれて増え方が小さくなってくるということです。

今、100万円を持っている人が100円をもらったとしても、そんなに嬉しいと思わないと思います。

しかし、今1000円しか持っていない人が100円をもらったら、100万円を持っている人よりも、より大きい喜びを感じるはずです。

お金を失う場合も同様で、100万円を持っている人が100円を落としたとしても、あまり悲しむことはないと思いますが、1000円しか持っていない人が100円を落とした場合、結構ショックを受けると思います笑

続いて、このグラフから分かることは、左右で線のカーブが異なるということです。

利得と書いてある右側の線よりも、損失と書いてある左側の線の方が、カーブがきつくなっています。

このとこから、我々人間は、お金を得る喜びよりも、お金を失う悲しもの方が大きく感じることがわかります。

そのため、この記事の冒頭でも紹介した通り、10万円を得る喜びよりも、10万円を失う悲しみの方が大きくなります。

価値関数では、お金を得る喜びよりも、お金を失う悲しみの方が2倍大きいと言われています。

確率加重関数

続いて、プロスペクト理論のもう一つの柱である、確率加重関数について紹介していきます。

確率加重関数は、人が感じる主観的な確率を表しています。

確率加重関数で使われる図がこちらです。

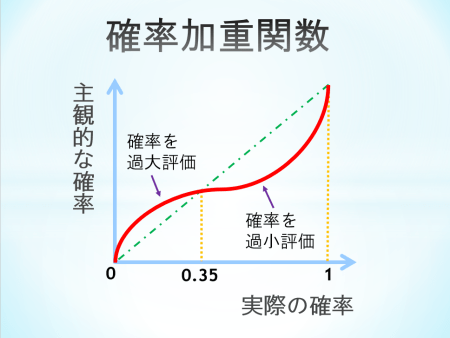
我々の確率の感じ方には、大きく分けて２つあります。

１つ目は、実際に起こる確率が低い時には、過大評価してしまい、実際よりも高い確率で起こると感じてしまうことです。

保険が例に挙げられます。

万が一のために、保険に加入しているという方は多いと思います。

しかし、その万が一が起こる確率はどれくらいでしょうか？

例えば、40歳の男性の死亡率は、「厚生労働省平成30年簡易生命表の概要」によると、0.00094％だそうです。

これは、10万人に1人の確率です。

しかし、0％に近いからこそ、我々は万が一が起こる確率を過大評価してしまいます。

そして、保険に入っていれば、万が一のことが起こっていも、損失をさけることができると考えるため、多くの人が保険に加入するのです。

もちろん、保険に加入することが悪いということではなく、あくまでも確率加重関数の一例だということをご理解ください(笑)。

他にも、宝くじなど、当たる確率はかなり低いのに、何となく当たる気がして買ってしまうのも、例に挙げられます。

続いて2つ目は、実際に起こる確率が中くらい以上になると、過小評価してしまい、実際よりも低い確率で起こると感じてしまうことです。

ポケモンのゲームをやったことがある方ならわかると思いますが、それぞれの技に命中率があります。

命中率が100％のものであればいいのですが、70％や85％だと、高い確率ではあるのに、何となく「外れるんじゃないか？」と低い確率を過大評価してしまったことがある方はいらっしゃると思います。

このように、我々は実際に起こる確率を見誤ってしまう傾向があり、特に0％か100％に近づくについて、その傾向が強くなっていきます。

プロスペクト理論の解説は以上です！

今回の内容をまとめます。

まず、プロスペクト理論とは、自分の選択の結果から得られる利益や被る損失、それらの確率によって、人がどのような選択をするのかを記述したものでした。

人間は、利益が得られる場面では危険回避的になり、損失を被りそうなときは危険愛好的になると言われています。

そして、プロスペクト理論には、価値関数と確率加重関数という2つの柱がありました。

価値関数では、平均的な利得が同じ場合であれば確実な選択を選び、平均的な損失が同じ場合はリスクが高い選択を選ぶ傾向があること、お金を得る喜びよりも、お金を失う悲しみの方が2倍大きいという2つの特徴が挙げられました。

確率加重関数では、実際に起こる確率が低い場合は過大評価してしまい、逆に確率が高い場合には過小評価してしまうという特徴が挙げられました。

全額返金保証を付けることによって、消費者の損をするかもしれないという気持ちをなくすことで買いやすくしたり、期間限定セールをすることで、今買わないと損だと思わせるなど、ビジネスの場でも使われています。

ぜひ、プロスペクト理論の知見を使って、様々なことに役立ててみてください！

私が実際に読んだ行動経済学の本をまとめて紹介しています！

よろしければ、こちらも参考にして下さい！

ではでは。